Перевод чисел из десятичной системы двоичную и обратно
В повседневной жизни мы привыкли пользоваться десятичной системой счисления, знакомой нам еще со школьной скамьи. Однако помимо нее, существует и множество других систем. Как записывать цифры не в десятичной, а, например, в двоичной системе?
Как перевести в двоичную любое число из десятичной системы
Необходимость перевести десятичное число в двоичный вид выглядит пугающей только на первый взгляд. На самом деле это довольно просто — необязательно искать даже онлайн-сервисы для совершения операции.
- Для образца возьмем число 156, записанное в привычной нам десятичной форме, и попробуем перевести его в двоичный вид.
- Алгоритм будет выглядеть следующим образом — начальное число понадобится разделить на два, затем еще раз на 2, и еще раз на 2 до тех пор, пока в ответе не останется единица.
- При совершении деления для перевода в двоичный код имеют значения не целые числа — а остатки. Если при делении в ответе получилось четное число, то остаток записывается в виде цифры 0, если нечетное — то в виде цифры 1.
- На практике можно легко убедиться, что начальный двоичный ряд остатков для числа 156 будет выглядеть следующим образом — 00111001. Для того, чтобы превратить его в полноценный двоичный код, этот ряд понадобится записать в обратном порядке — то есть, 10011100.
Двоичное число 10011100, полученное в результате нехитрой операции, и будет двоичным выражением числа 156.
Ещё один пример, но уже на картинке
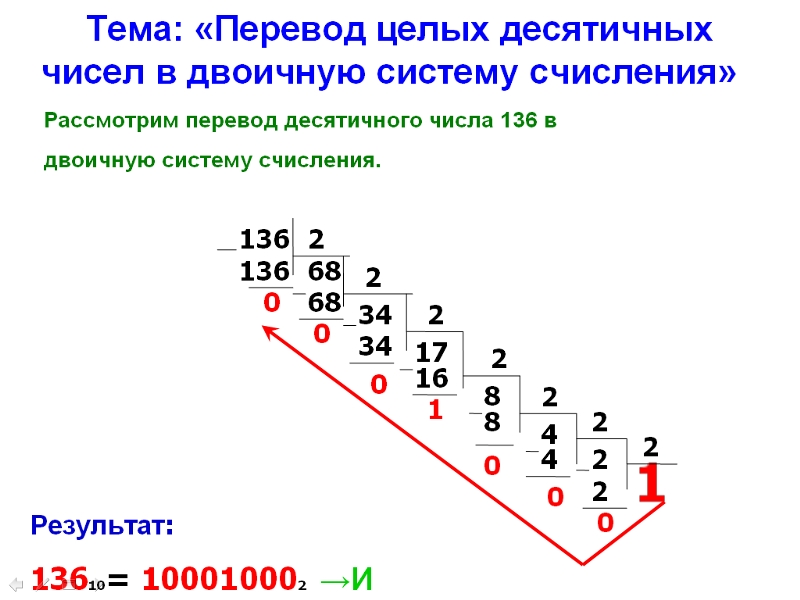
Перевод двоичного числа в десятичную систему
Обратный перевод — из двоичной в десятичную систему — может показаться чуть более сложным. Но если использовать простой метод удвоения, то и с этой задачей получится справиться за пару минут. Для примера возьмем все то же число, 156, но в двоичном виде — 10011100.
- Метод удвоения основан на том, что при каждом шаге вычисления берут так называемый предыдущий итог и прибавляют к нему следующую цифру.
- Поскольку на первом шаге предыдущего итога еще не существует, здесь всегда берут 0, удваивают его и прибавляют к нему первую цифру выражения. В нашем примере это будет 0 * 2 + 1 = 1.
- На втором шаге мы уже располагаем предыдущим итогом — он равен 1. Это цифру нужно удвоить, а потом прибавить к ней следующую по порядку, то есть — 1 * 2 + 0 = 2.
- На третьем, четвертом и последующем шагах все так же берутся предыдущие итоги и складываются с последующей цифрой в выражении.
Когда в двоичной записи останется только одна последняя цифра, и прибавлять больше будет нечего, операция будет завершена. При помощи нехитрой проверки можно убедиться, что в ответе получится нужное десятичное число 156.
