Теорема Пифагора – формулировка и доказательство
Древнегреческий мыслитель Пифагор прославился многими открытиями в точных науках. Но наибольшей известностью пользуется его теорема для прямоугольных треугольников. Она очень проста для понимания, легко доказывается, и проходят ее еще в 8 классе школы.

Разберемся, как именно звучала теорема Пифагора в старые времена, как выглядит ее определение в наши дни, и каким образом можно ее доказать.
Зависимость между площадями квадратов катетов и гипотенузы
Изначально формулировка правила, выведенного Пифагором, звучала так: если построить на гипотенузе треугольника с прямым углом квадрат, то площадь его будет точно равна площадям двух квадратов, построенных на катетах, сложенным между собой.
В современной геометрии определение звучит немного проще и более формально: для треугольника с прямым углом будут равны квадрат гипотенузы и сложенные вместе квадраты катетов.
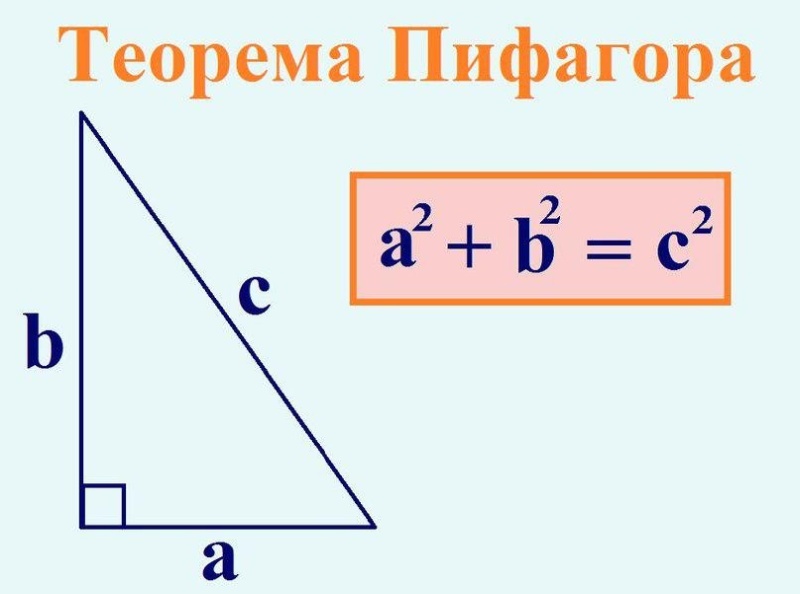
Как доказать эту теорему? Способов существует несколько, но наиболее распространен следующий из них:
- выстраивают прямоугольник АВС, где С — прямой угол;
- от угла С к стороне АВ, или гипотенузе, проводят высоту и обозначают ее, как Н;
- в результате получают два прямоугольных треугольника внутри АВС — треугольник АСН и треугольник СВН;
- при этом АСН по признаку двух углов подобен АВС, таким же образом СВН подобен АВС;
- сторону ВС условно обозначают, как «а», сторону АС — как «b», сторону АВ — как «с»;
- по принципу подобия получается, что а/с = НВ/а, а b/c = AH/b;
- из этого следует, что a2 = c * HB, в то время как b2 = c * AH.
Дальше остается сложить полученные равенства. Выглядит это следующим образом: a2 + b2 = c*HB + c*AH, или a2 + b2 = c*(HB + AH), или а2 + b2 = c*AB, или а2 + b2 = c*c, и наконец, а2 + b2 = c2.
Именно это и требовалось доказать. Квадрат гипотенузы в решении получился равен квадратам катетов, сложенным между собой.
Интересно, что на данный момент существует свыше 300 самых разных доказательств знаменитой теоремы — и все они верны. Если попробовать поискать доказательства в Интернете, то десятки сайтов предложат тригонометрические, геометрические, алгебраические варианты разного уровня сложности. Огромное количество доказательств свидетельствует о том, что теорема Пифагора действительно неоспорима — и более того, является фундаментом для всей геометрической науки. При дальнейшем изучении предмета становится ясно, что из данной теоремы выходит и очень много следствий.
