Решение системы линейных уравнений методом обратной матрицы
Метод обратной матрицы не представляет ничего сложного, если знать общие принципы работы с матричными уравнениями и, конечно, уметь производить элементарные алгебраические действия.
Решение системы уравнений методом обратной матрицы. Пример.Удобнее всего постигать метод обратной матрицы на наглядном примере. Возьмем систему уравнений:
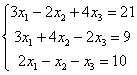
Первый шаг, который необходимо сделать для решения этой системы уравнений — найти определитель. Поэтому преобразим нашу систему уравнений в следующую матрицу:
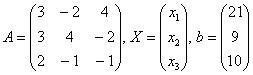
И найдем нужный определитель:
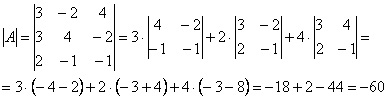
Формула, использующаяся для решения матричных уравнений, выглядит следующим образом:
Х = А-1b.
Таким образом, для вычисления Х нам необходимо определить значение матрицы А-1 и умножить его на b. В этом нам поможет другая формула:
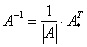
Ат в данном случае будет транспонированной матрицей — то есть, той же самой, исходной, но записанной не строками, а столбцами.
Не следует забывать о том, что метод обратной матрицы, как и метод Крамера, подходит только для систем, в которых определитель больше или меньше нуля. Если же определитель равен нулю, нужно использовать метод Гаусса.
Следующий шаг — составление матрицы миноров, представляющей собой такую схему:
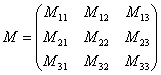
В итоге мы получили три матрицы — миноров, алгебраических дополнений и транспонированную матрицу алгебраических дополнений. Теперь можно переходить к собственно составлению обратной матрицы. Формулу мы уже знаем. Для нашего примера это будет выглядеть так:
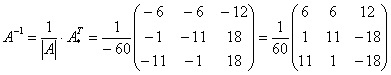
Работа почти закончена. Теперь осталось выполнить только умножение матрицы.
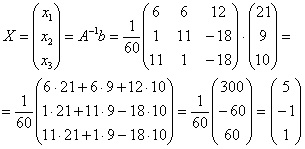
Таким образом, ответ для взятого нами примера получается следующим: х1 = 5, х2 = -1, х3 = 1.
