Решение систем линейных уравнений методом Гаусса
Метод Гаусса не требует никаких глубоких математических познаний и доступен практически каждому — достаточно просто понимать алгоритм вычислений и справляться с простейшими действиями, такими, как сложение и умножение. Кроме того, этот метод подходит для тех случаев, когда применить методы Крамера или обратной матрицы невозможно по условию задачи.
Рассмотрим решение систем уравнений методом Гаусса на примере.
Пример решения систем линейных уравнений методом Гаусса.
Изучим принцип работы метода на примере, взяв следующую систему уравнений:
Первое, что нужно сделать — это записать нашу задачу в виде матрицы расширенного вида — иначе говоря, оставить в уравнениях только числовые коэффициенты.

Затем при помощи элементарных преобразований получившаяся матрица приводится к виду «треугольника». Делается это в несколько шагов:
1. Первая и вторая строки матрицы меняются местами.
2. Во вторую, третью и четвертую строку добавляются элементы первой строки, умноженные на – 5, - 3 и - 4.
3. Вторая и третья строки снова меняются местами, в то время как к третьей и четвертой добавляются элементы второй строки (умноженные на 4 и 1).
4. Затем из четвертого уравнения вычитается третье (умноженное на 11 и – 3).
Записывается все это следующим образом:

Получившаяся матрица переводится обратно в исходную систему уравнений:
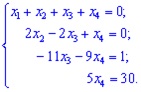
Как видно по картинке, мы получили искомый «треугольник».
Теперь остается только решить простейшие уравнения.
5х4 = 30, следовательно, х4 = 6. Подставляем результат в третью строку:

Теперь, опираясь на полученные результаты, решаем уравнение из второй строки:

И последний шаг — найти значение х1, что не составит никакого труда, учитывая уже имеющиеся у нас данные:

Система уравнений полностью решена. Можно записывать ответ: х1 = 7, х2 = - 8, х3 = - 5, х4 = 6.
