Решение линейных уравнений методом Крамера
Правило крамера.
Среди способов решения линейных уравнений — не только методика Гаусса и метод обратной матрицы, но и правило Крамера. Метод основан на работе с определителями и позволяет легко решить систему уравнений.
Следует отметить, что метод Крамера подходит только для тех ситуаций, когда определитель не равен нулю. В ином случае придется использовать метод Гаусса.
Итак, как же решается система линейных уравнений по методу Крамера?
Решение линейных уравнений по Крамеру.
Пример решения системы линейных уравнений методом Крамера.
Разберем на примере.
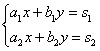
Первый этап работы — это вычислить главный определитель системы, в нашем случае:
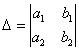
Как уже было сказано, если определитель системы равен нулю, то метод Крамера не подходит для работы, поскольку выходит, что система или не имеет решений, или имеет бесконечное множество их. В таком случае используется метод Гаусса.
Если же определитель больше или меньше нуля, то методом Крамера мы можем вычислить единственное верное решение. Для этого необходимо найти еще два определителя системы:

Теперь остается лишь найти корни уравнения, а они рассчитываются по следующим формулам:
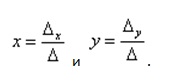
Рассмотрим еще один пример. Возьмем систему линейных уравнений:
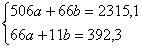
Метод Крамера – наиболее удобный метод как раз для работы со сложными уравнениями, включающими в себя десятичные дроби. Иные методы оказываются сложнее, да и в вычислениях можно просто запутаться. Здесь же все довольно просто. Находим главный определитель:
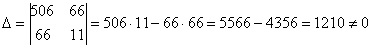
Определитель не равен нулю, следовательно, система имеет решение, и мы можем найти его методом Крамера.

Таким образом, получаем, что а = - 0,35, в = 37,77. Система линейных уравнений полностью решена, можно записывать ответ.
