Линейные уравнения
Линейные уравнения — относительно несложная математическая тема, довольно часто встречающаяся в заданиях по алгебре. Разберемся, что это такое, и как решаются линейные уравнения.
Как правило, линейное уравнение — это уравнение вида ax + c = 0, где а и с — произвольные числа, или коэффициенты, а х — неизвестное число.
К примеру, линейным уравнением будет:
2х + 4 = 0,
или
5х + 8 = 0,
или
4х + 1 = 0,
И так далее.
Решение линейных уравнений.
Как решать линейные уравнения?
Решаются линейные уравнения совсем несложно. Для этого используются такой математический прием, как тождественное преобразование. Разберем, что это такое.

Пример линейного уравнения и его решение.
Пусть ax + c = 10, где а = 4, с = 2.
Таким образом, получаем уравнение 4х + 2 = 10.
Для того чтобы решить его было проще и быстрее, воспользуемся первым способом тождественного преобразования — то есть, перенесем все цифры в правую часть уравнения, а неизвестное 4х оставим в левой части.
Получится:
4х = 10 – 2,
4х = 8.
Таким образом, уравнение сводится к совсем простенькой задачке для начинающих. Остается лишь воспользоваться вторым способом тождественного преобразования — оставив в левой части уравнения х, перенести в правую часть цифры. Получим:
Х = 8 : 4,
Х = 2.
Проверка:
4х + 2 = 10, где х = 2.
4 * 2 + 2 = 10.
8 + 2 = 10.
Ответ верный.
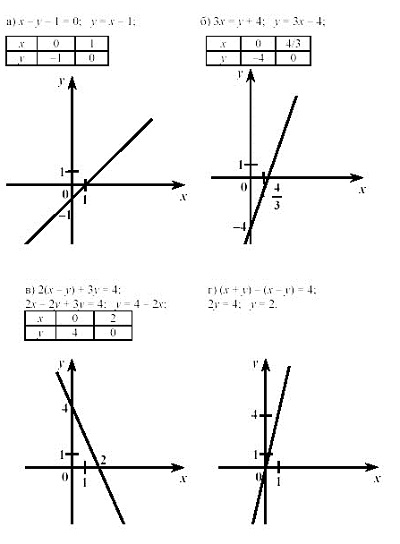
График линейного уравнения.
При решении линейных уравнений с двумя переменными также часто используется метод построения графика. Дело в том, что уравнение вида ах + ву + с = 0, как правило, имеет много вариантов решения, ведь на место переменных подходит множество чисел, и во всех случаях уравнение остается верным.
Поэтому для облегчения задачи выстраивается график линейного уравнения.
Чтобы построить его, достаточно взять одну пару значений переменных — и, отметив их точками на плоскости координат, провести через них прямую. Все точки, находящиеся на этой прямой, и будут вариантами переменных в нашем уравнении.